알고리즘
0

알고리즘 - 1
백준 1197번 - 최소 스패닝 트리
by HOON
0
Last updated on June 18, 2024, 9:15 p.m.
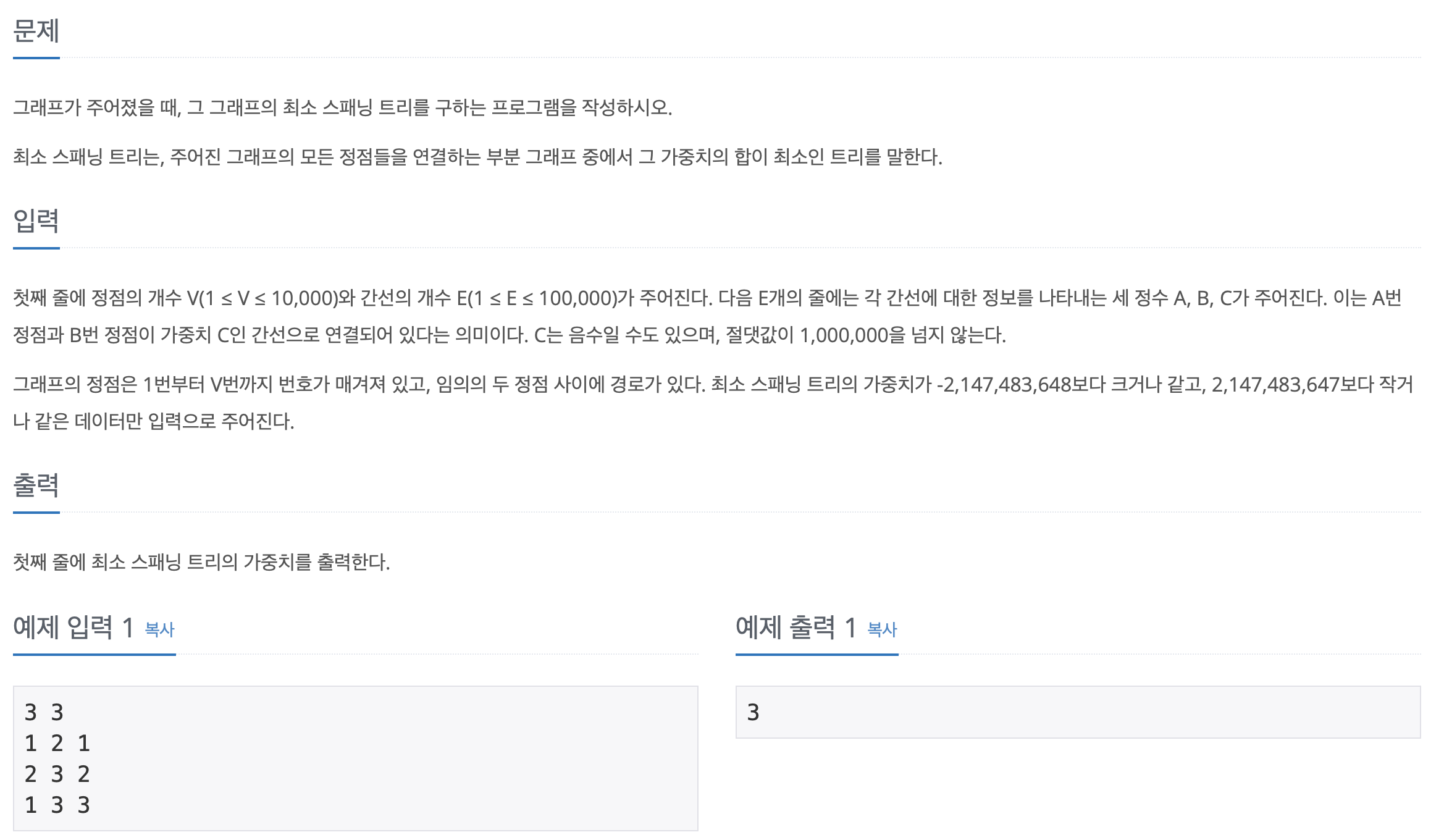
문제
해당 문제는 정점(V)와 간선(E)가 주어질 때, 최소 스패닝 트리를 사용하여 간선의 최소 합을 요구하는 문제입니다.
그럼 여기서, 최소 스패닝 트리란?
모든 정점이 연결되어있고, 사이클이 존재하지 않는 경우를 말합니다.
예를들면, 모든 도시가 연결되어있을 때 최소비용을 구할 때가 있겠네요.
풀이
최소 스패닝 트리를 구현하는데에는 두 가지 알고리즘이 있습니다.(크루스칼 알고리즘, 프림 알고리즘)
여기서는 크루스칼 알고리즘을 사용하여 구현하겠습니다.
크루스칼 알고리즘의 순서는 아래와 같습니다.
- 주어진 간선을 최소 비용으로 먼저 sort
- sort된 순서대로 간선을 선택하면서, 싸이클이 생성되는지 확인합니다.(union_path 기법)
순서를 토대로 코드를 작성해보면
'''
3 3
1 2 1
2 3 2
1 3 3
'''
import sys
input=sys.stdin.readline
V,E = map(int,input().split())
parent=[0]*(V+1)
graph=[]
result=0
#부모 노드 찾기
def find_parent(parent,x):
if parent[x]!=x:
parent[x] = find_parent(parent,parent[x])
return parent[x]
#두 원소가 속한 부모노드 합치기
def union_parent(parent,a,b):
a = find_parent(parent,a)
b = find_parent(parent,b)
if a<b:
parent[b] = a
else:
parent[a] = b
#부모테이블 부모를 자기자신으로 초기화
for i in range(1,V+1):
parent[i]=i
#정점,간선 설정
for _ in range(E):
a,b,cost = map(int,input().split())
graph.append((cost,a,b))
graph.sort()
for edge in graph:
cost,a,b = edge
#부모노드가 같지 않을경우에, 즉 사이클이 이뤄지지 않을때만
if find_parent(parent,a) != find_parent(parent,b):
union_parent(parent,a,b)
result+=cost
print(result)
이렇게 작성 할 수 있습니다.
부모노드는 각 정점별 방문 시 사이클이 존재하는지의 여부를 확인하기 위함입니다.
따라서 부모노드가 같지 않을경우, 즉 사이클이 존재하지 않을때만 비용을 늘려가는 식으로 구현하면 됩니다.
×
![]()
Leave a Comment: